Числа, які використовуються при лічбі, 1, 2, 3, 4, … називаються натуральними числами.
Найменше число – 1, найбільшого числа не існує.
Властивості додавання:
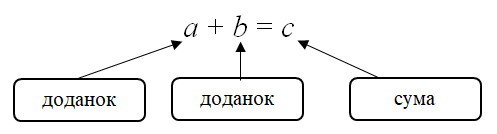
- переставна властивість a + b = b + a (від перестановки доданків сума не змінюється)
- сполучна властивість (a + b) + c = a + (b + c) (щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого і третього)
Властивості віднімання:
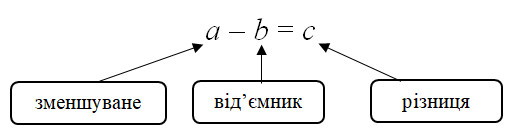
- властивість віднімання суми від числа a – (b + c) = (a – c) + b, або (a + b) – c = (a – c) – b (щоб відняти суму від числа, можна від нього відняти один з доданків, а потім від результату відняти другий доданок)
- властивість віднімання числа від суми (a + b) – c = (a – b) – c, або a – (b + c) = (b – c) + a (щоб відняти число від суми, можна відняти його від одного з доданків і до результату додати другий доданок)
Властивості множення:
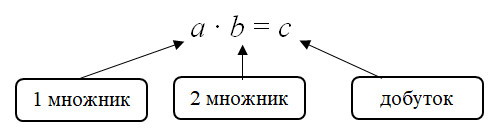
- переставна властивість a ∙ b = b ∙ a (від перестановки множників добуток не змінюється)
- сполучна властивість (a ∙ b) ∙ c = a ∙ (b ∙ c) (щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого і третього)
- розподільна властивість (a + b) ∙ c = a ∙ b + a ∙ c (щоб помножити суму на число, можна помножити на це число кожний доданок і ці добутки додати)
- розподільна властивість (a – b) ∙ c = a ∙ b – a ∙ c (щоб помножити різницю на число, можна помножити на це число зменшуване і від’ємник і від першого добутку відняти другий)
- a ∙ 1 = a
- a ∙ 0 = 0
Добуток двох однакових чисел, називається квадратом числа (a2)
Добуток трьох однакових чисел, називається кубом числа (a3)
Властивості ділення:
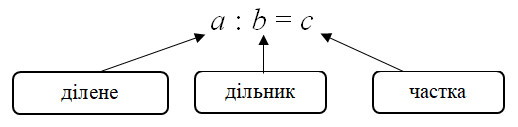
- a : 1 = a
- a : 0 = не існую (на 0 ділити не можна)
- 0 : a = 0
Джерела: https://uk.wikipedia.org



Тест пройшла